Question

Chris is making a capacitor with capacitance of 1 microfarad. The voltage across the plates is 9 volts. How many electrons need to be on the negatively charged plate? The charge of an electron is 1.6 × 10–19 coulombs.

5.6 × 10 ^13 electrons
1.4 × 10 ^-24 electrons
9.0 × 10 ^-6 electrons
1.4 × 10 ^-18 electrons

Answer 1

Capacitance is given by

`C= (Q)/(V)`
where Q is the total charge on a plate and V is the voltage across the plates. Here, Q is the charge on the electron times the number of electrons, or

`C= (Nq)/(9.0V) =1 \mu F`
Solving for N, the total number of electrons:

`N= \frac{1.0E-6F * 9.0V} {1.6E-19C}=5.6 * 10^(13)`

Answer 2

Explanation :

Capacitance of a capacitor,
`C=1\ \mu F=10^(-6)\ F`

Potential across the plates,
`V=9\ V`

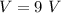
We know that the capacitance of a capacitor is given by :

`q=CV`

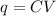
We have to find the number of electrons.

since, q = ne (Charge is quantised)

n is the number of electrons.

So, ne = CV

`n=(CV)/(e)`

`n=(10^(-6)\ F* 9\ V)/(1.6* 10^(-19)\ C)`

`n=5.625* 10^(-13)`

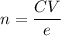
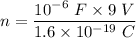
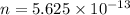
or

`n=5.6* 10^(-13)`

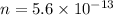
So, the no. of electrons need to be on the negatively charged plate is
`5.625* 10^(-13)`.

Hence, this is the required solution.