Question

Find the number of distinguishable permutations of the letters in the word supercalifragilisticexpialidocious?

Answer 1

"supercalifragilisticexpialidocious" has 34 letters, with 10 letters that appear more than once. In all, there are
`34!` permutations if we consider each letter to be distinct from any other, even duplicate letters.

If we assume duplicate letters are indistinguishable, then we need to divide this total by the number of ways we can permute those duplicate letters. For instance, the binary string 101 has
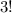
`3!` possible permutations, but in each permutation, we can rearrange the 1s in
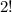
`2!` ways (e.g. 101* and 1*01).

So in the word "supercalifragilisticexpialidocious", we have:

2 copies each of e, o, p, r, u;
3 copies each of a, c, l, s;
7 copies of i;

which means we have a total of


`(34!)/((2!)^5(3!)^47!)=1,412,469,529,257,855,275,311,104,000,000`

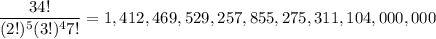
possible permutations if we consider any duplicate letters identical.

Answer 2

1,412,469,529,257,855,275,311

Explanation:

Find the number of distinguishable permutations of the letters in the word supercalifragilisticexpialidocious?

supercalifragilisticexpialidocious is about 34 characters

some letters appear more than once

they are

e, o, p, r, u; 2 copies

a, c, l, s; 3 copies

i- 7 copies

The permutations will be then

(
`(34!)/((2!)^5(3!)^4(7!))`

SO WE HAVE

1,412,469,529,257,855,275,311 ways are the number of ways we can arranged the word supercalifragilisticexpialidocious.