Question

How many different committees can be formed from 99 teachers and 3434 students if the committee consists of 33 teachers and 22 ​students?

Answer 1

47,124 committees.

Step-by-step explanation:

We are asked to find the number of different committees that can be formed from 9 teachers and 34 students if the committee consists of 3 teachers and 2 ​students.

To solve our given problem we will use combination formula:

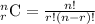`_(r)^(n)\textrm{C}=(n!)/(r!(n-r)!)`, where,

n= Total number of items,

r = Number of items being chosen at a time.

Since we are choosing 3 teachers from 9 teachers and 2 students from 34 students, so we can represent this information as:

`_(3)^(9)\textrm{C}* _(2)^(34)\textrm{C}=(9!)/(3!(9-3)!)* (34!)/(2!(34-2)!)`

`_(3)^(9)\textrm{C}* _(2)^(34)\textrm{C}=(9!)/(3!(6)!)* (34!)/(2!(32)!)`

`_(3)^(9)\textrm{C}* _(2)^(34)\textrm{C}=(9*8*7*6!)/(3*2*1(6)!)* (34*33*32!)/(2*1(32)!)`

`_(3)^(9)\textrm{C}* _(2)^(34)\textrm{C}=3*4*7* 17*33`

`_(3)^(9)\textrm{C}* _(2)^(34)\textrm{C}=47,124`

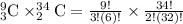
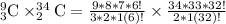
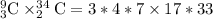
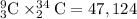
Therefore, 47,124 different committees can be formed from 9 teachers and 34 students.

Answer 2

There are 47,124 different committees you can select.

Step-by-step explanation:
The number of combinations of 9 teachers taken 3 at a time is given by

`_9C_3=(9!)/(3!6!)=84`

The number of combinations of 34 students taken 2 at a time is given by

`_(34)C_2=(34!)/(2!32!)=561`

Together this makes 84*561 = 47124 combinations.