Question

The population of Ashmore was 925 in 2000 and in 1028 in 2001. the linear model for ashmores population is p= 103t+925, where the is the years since 2000.

Find an exponential model, in the form pm a (b)^2, for ashmores population t-ywars after 2000. round b to the nearest thousandth.

How much greater is the population predicted by the exponential model than that predicted by the linear model for the year 2015?

Answer 1

exponential population is 2035 greater than the linear model.

Explanation:

Exponential modal for the population of Ashmore given in the question after 2000 is in the form of population =
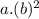`a.(b)^(2)` Or we can the equation in the form of population =
`a.(r)^(t)`

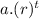
where "a" is the population of Ashmore in 2000 = 925

r = common ration = 1028/925 = 1.1113

t = years

Now we have to calculate the population for the year 2015

`=925.(1.1113)^(15)`

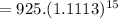
= 925 × 4.87 = 4505

population predicted by linear model for year 2015

p = 103t + 925

p = 103×15 + 925

p = 2470

Now the difference in exponential model and linear model will be

= 4505 - 2470 = 2035

Answer 2

divide known populations:

1028 / 925 = 1.11135

so exponential formula would be 925*1.11135^t

using 15 years: 925 * 1.11135^15 = 4507

linear model: 103(15) +925 = 2470

4507 - 2470 = 2037 more people using exponential