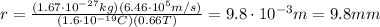Question

Find the radius of a proton's orbit when it moves perpendicular to a magnetic field of 0.66 t with a speed of 6.46×105 m/s .

Answer 1

The centripetal force that keeps the proton in circular orbit is provided by the Lorentz force exerted by the magnetic field:

`m (v^2)/(r) = qvB`
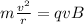
where m is the mass of the proton, v its speed, q its charge and B the magnetic field intensity.
By re-arranging the formula, we have:

`r= (mv)/(qB)`

Using B=0.66 T and
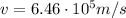
`v=6.46 \cdot 10^5 m/s`, we find the radius of the proton's orbit:

`r= ((1.67 \cdot 10^(-27)kg)(6.46 \cdot 10^5 m/s))/((1.6 \cdot 10^(-19)C)(0.66 T))=9.8 \cdot 10^(-3)m=9.8 mm`