Question

The function h(t)=-4.92t^2+14.69t+575 is used to model an object being tossed from a tall building, where h(t) is the height in meters and t is the time in seconds. Rounded to the nearest hundredth, what are the domain and range?

Answer 1

Domain is the set of all real numbers.

Range is the set of all real numbers h(t) such that h(t) ≤ 585.97

Explanation:

Given function,

`h(t)=-4.92t^2+14.69t+575`,

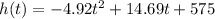Which is a polynomial,

∵ The domain of a polynomial is the set of all real numbers,

So, the domain of the given function is the set of all real numbers,

Now, the coefficient of
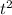`t^2` is negative, so, it is an open downward parabola having vertex (1.493, 585.965),

Since the value of h(t) is maximum at its vertex,

Hence, the value of h(t) is less than or equal to 585.965,

Therefore, the range of the above function is set of all real numbers h(t) such that, h(t) ≤ 585.97

Answer 2

Given that equation modelling the height of the building is given by:
h(t)=-4.92t^2+14.69t+575
plotting the equation (see the plot below)
The domain in all real numbers.

Range: (h∈R: 196800h≤115317961)