Final answer:
Using the principle of similar triangles, the tree's height is calculated to be 132 inches, based on the given measurements of Corey's height and the lengths of the shadows.
Step-by-step explanation:
Corey is 66 inches tall and his shadow is 108 inches long. At the same time, a tree casts a shadow that is 216 inches long. Since the right triangles formed by Corey and the tree with their respective shadows are similar, we can use proportions to find the height of the tree.
Let x represent the height of the tree. Setting up a proportion based on the similar triangles, we have:

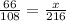
Cross-multiplying to solve for x gives us:
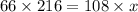
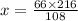

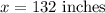
Therefore, the tree's height is 132 inches tall.