Question

For f(x)= 3x+1 and g(x)= x^2-6, find (g/f)(x).

A. 3x+1/x^2-6 , x≠ ±√6

B. 3x+1/x^2-6

C. x^2-6/3x+1

D. x^2-6/3x+1, x≠ -1/3

Answer 1

`A. (x^2+6)/(3x+1), x\\eq -(1)/(3)`

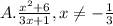
Explanation:

Given functions,

`f(x) = 3x + 1`

`g(x) = x^2 - 6`

∵
`((g)/(f))(x) = (g(x))/(f(x))`

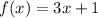
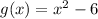
By substituting the values,

`((g)/(f))(x)=(x^2-6)/(3x+1)`

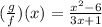
Which is a rational function,

We know that,

A rational function is defined for all real numbers except those for which denominator = 0,

If
`3x+1 = 0`

`\implies 3x = -1`

`\implies x =-(1)/(3)`

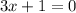
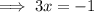
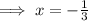
i.e. domain restriction of g/f is x≠ -1/3

Hence, OPTION D is correct.

Answer 2

D. The exclusion is important because we cannot divide by zero. Apart from that we are simply looking at a function.