your inequality would look like
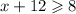
to solve, you need to subtract 12 from both expressions leaving x isolated on the left and -4 on the right
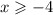
what this means is your solution for x is any number that is -4 or greater.
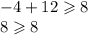
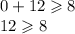
if you put a value in for x that is lower that -4, the inequality will not be true.
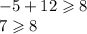
since 7 is not greater than or equal to 8, the value of -5 is not a solution for x in the inequality