Question

A formula is expressed as d=a(2+kt). Express k in terms of d, a and t

Answer 1

`k=(d)/(ta)-(2)/(t)`

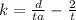
Step-by-step explanation:

d=a(2+kt)

WE need to solve for k. our aim is to get K alone

d= a(2+kt)

To eliminate 'a' we divide by 'a' on both sides

`(d)/(a) = 2+ kt`

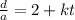
To eliminte 2 we subtract 2 on both sides

`(d)/(a)-2 =kt`

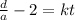
Now to isolate K we divide by 't' on both sides

When we divide a fraction by 't' then we multiply 't' at the bottom

`(d)/(ta)-(2)/(t)=k`

Answer 2

Answer:
k =
`(d-2a)/(at) = (d)/(at) - (2a)/(at) = (d)/(at) - (2)/(t)`

Step-by-step explanation:
To get the value of k, we will need to isolate it on one side of the equation.
This can be done as follows:
d = a(2+kt)

1- get rid of the brackets using distributive property:
d = a(2+kt)
d = 2a + akt

2- Subtract 2a from both sides of the equation:
d - 2a = 2a + akt - 2a
d - 2a = akt

3- Divide both sides of the equation by "at":

`(d-2a)/(at) = (akt)/(at)`


`k= (d-2a)/(at)`

4- We can further simplify the answer as follows:
k =
`(d-2a)/(at) = (d)/(at) - (2a)/(at) = (d)/(at) - (2)/(t)`

Hope this helps :)