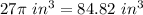Question

A candle manufacturer sells cylindrical candles in sets of three. Each candle in the set is a different size. The smallest candle has a radius of 0.5 inches and a height of 3 inches. The other two candles are scaled versions of the smallest, with scale factors of 2 and 3. How much wax is needed to create one set of candles?

Answer 1

Each candle in the set is a different size.
The smallest candle has a radius of 0.5 inches and a height of 3 inches.
The other two candles are scaled versions of the smallest, with scale factors of 2 and 3.
How much wax is needed to create one set of candles?
in cubic inches
Answer

pi 0.5^2 *3 = 0.75pi is the volume of the first candle.
The second volume is 8 * 0.75pi = 6pi.
And the last volume is 27 * 0.75 pi = 20.25 pi So in total we just take the sum and that is 27pi

Answer 2

To create one set of candles is needed
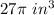`27\pi\ in^(3)` or
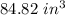`84.82\ in^(3)` of wax

Explanation:

we know that

The volume of a cylinder is equal to

`V=\pi r^(2) h`

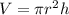
step 1

Find the volume of the smallest candle

we have

`r=0.5\ in`

`h=3\ in`

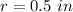
substitute

`V=\pi (0.5^(2))(3)=0.75 \pi\ in^(3)`

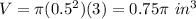
step 2

Find the volume of the second candle

Remember that

If two figures are similar, then the ratio of its volumes is equal to the scale factor elevated to the cube

we have

the scale factor is equal to
`2`

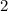
The volume of the second candle is equal to

`2^(3) *0.75\pi =6\pi\ in^(3)`

step 3

Find the volume of the third candle

Remember that

If two figures are similar, then the ratio of its volumes is equal to the scale factor elevated to the cube

we have

the scale factor is equal to
`3`

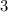
The volume of the third candle is equal to

`3^(3) *0.75\pi =20.25\pi\ in^(3)`

step 4

To find the total wax needed, sum the volume of the three candles

so

`0.75\pi\ in^(3)+6\pi\ in^(3)+20.25\pi\ in^(3)=27\pi\ in^(3)`

`27\pi\ in^(3)=84.82\ in^(3)`