Answer:
The options modeling a linear function are 1, 2, 3 and 5.
Explanation:
We know that,
A linear function is of the form
 , where a, b are fixed constants.
, where a, b are fixed constants.
Now, according to the options, we have,
1) The cost per visit to a community pool.
Let, x= number of visits to the pool and 'a'= fixed cost of visit.
Then, the cost per visit to the pool y, is
 .
.
So, this represents a linear function.
2) The neighborhood charges a yearly fee to use the pool.
Let, x= number of years and 'a'= fixed fee to use the pool
Then, the yearly fee to use the pool y, is
 .
.
So, this represents a linear function.
3) The cost to attend a show at the local theater. Tickets are $12 each.
Let x= number of shows and the cost of one show is $12.
Then, the cost of 'x' shows y, is

So, this represents a linear function.
4) An endangered species population is decreasing by 15% each year.
Let, a= initial population of the species and x= number of years.
The decrease rate = 15% = 0.15
So, the decrease in the population (y) is given by,
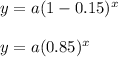
So, this does not represents a linear function.
5) The distance a bicyclist travels when cycling at a constant speed of 30 mph.
Let, x= time and the speed of the cyclist = 30 mph.
So, the distance (y) is given by,
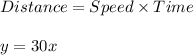
So, this represents a linear function.
6) The population of a town growing at a constant rate each year.
Let, a= initial population of the species and x= number of years and r= constant increase rate per year.
So, the increase in the population (y) is given by
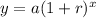
So, this does not represents a linear function.
Thus, the options modeling a linear function are 1, 2, 3 and 5.