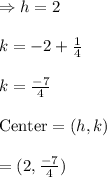Answer with explanation:
The Information about the given Parabola:
→Opens Upward
→Passes through the point (3,-1).
→Vertex is at (2,-2).
Equation of Parabola , having vertex at , (2,-2) and opening Upwards is given by:
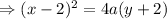
The Parabola passes through the point (3,-1).
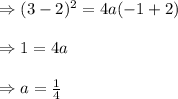
So,Required Equation of Parabola will be
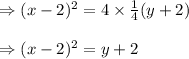
Center of the Parabola called focus will be