Question

2. Factor f(x) = x4 + 10x3 + 35x2 + 50x + 24 completely showing all work and steps with synthetic division. Then sketch the graph. please use synthetic division

Answer 1

We need to use rational root theorem to find out roots here.

The rational root theorem states that if p(x) is a polynomial with integer coefficients and if
`(p)/(q)` is a zero of p(x) then p is a factor of constant term and q is a factor of leasing term coefficient.

Here factors of constant term are 1,2,3,4,6,8,12,24,-1,-2,-3,-4,-6,-8,-12, and -24.

And factors of leading coefficient is -1,1.

Hence possible roots may be -1,1,-2,2,-3,3,-4,4,-6,6,-8,8,-12,12,-24 and 24.

Let us plugin these in f(x) to find zeroes.

`f(-1)=(-1)^(4)+10(-1)^(3)+35(-1)^(2)+50(-1)+24 =1-10+35-50+24=0`

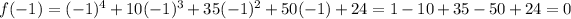
Hence x=-1 is a zero which means x-(-1)=x+1 is a factor.

Let us use synthetic division to find quotient.

-1 | 1 10 35 50 24

| 0 -1 -9 -26 -24

1 9 26 24 0

Hence quotient is
`x^(3) +9x^(2) +26x+24`

Since all coefficients are positive, root must be negative. Let's plugin all remaining negative numbers in the quotient.

`(-2)^(3)+9(-2)^(2)+26(-2)+24 = 0`

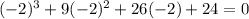
Hence x+2 is another factor.

Let us find quotient again using synthetic division.

-2 | 1 9 26 24

| 0 -2 -14 -24

1 7 12 0

Hence quotient is
`x^(2) +7x+12`

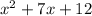
Again we got quotient with all positive coefficients, let us plugin remaining negative numbers from rational root theorem.

`(-3)^(2)+7(-3)+12=-9-21+12=0`

Hence x+3 is also a factor.

Let us find quotient using synthetic division.

-3 | 1 7 12

| 0 -3 -12

1 4 0

Hence quotient is x+4.

So,
`f(x)=x^(4)+10x^(3)+35x^(2)+50x+24 =(x+1)(x+2)(x+3)(x+4)`

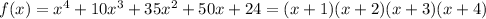
Please have a look at the graph attached.