Question

Completely factor the polynomial 8x2 – 24x + 20x – 60. 8x(x + 3)(x – 5) (4x – 3)(2x – 5) 2(2x – 3)(2x + 5) 4(x – 3)(2x + 5)

Answer 1

D

Explanation:

Answer 2

8x2 – 24x + 20x – 60

We are given the expression:

`8x^(2)-24x+20x-60`

Now we have to perform following steps here:

Step 1: Find the GCF

The GCF here is 4, so taking out the GCF

`8x^(2)-24x+20x-60`

=
`4(2x^(2)-6x+5x-15)`

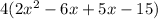
Step 2: Factor by grouping

Group first two terms together and last two terms together,

`4[(2x^(2)-6x)+(5x-15)]`

Now factor each group by finding GCF,

`4[(2x(x-3)+5(x-3)]`

=
`4[(2x+5)(x-3)]`

Answer: The final factorised form is
`4[(2x+5)(x-3)]`.