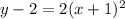Question

The minimum of the graph of a quadratic function is located at (-1,2) . the point (2,20) is also shown on the parabola . which function represents the situation?

Answer 1

Explanation:

Given that The minimum of the graph of a quadratic function is located at (-1,2)

This implies that parabola is open up.

Hence parabola would have equaiton of the form

`y-2 = 4a(x+1)^2`

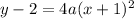
To find a:

We use the fact that the parabola passes through (2,20)

Substitute x=2 and y =20

`20-2 = 4a(2+1)^2\\18 =36a\\a = 0.5`

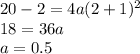
Hence equation would be

`y-2 = 2(x+1)^2`

Answer 2

the complete question in the attached figure

we know that
the equation of a parabola is
y=a(x-h)²+k
where
(h,k) is the vertex --------> (h,k)--------> (-1,2)
so
y=a(x+1)²+2

point (2,20)
for x=2
y=20
20=a(2+1)²+2--------> 20=a*9+2--------> 9*a=18---------> a=2

the equation of a parabola is
y=a(x+1)²+2-------> y=2(x+1)²+2

therefore

the answer is the option
C) f(x) = 2(x + 1)2 + 2