Question

Express the complex number in trigonometric form. 2 - 2i

Answer 1

Substitute the values of θ=−π4θ=-π4 and |z|=2√2|z|=22.2√2(cos(−π4)+isin(−π4))

Answer 2

The trigonometric form is
`z=2√(2)(\cos((\pi)/(4))+i\sin((\pi)/(4)))`.

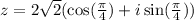Explanation:

To find : Express the complex number in trigonometric form 2 - 2i ?

Solution :

First we find the modulus of complex number

If
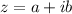`z=a+ib` then the modulus is
`|z|=√(a^2+b^2)`

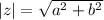
On comparing, a=2, b=-2

So,
`|z|=√(2^2+(-2)^2)`

`|z|=√(4+4)`

`|z|=2√(2)`

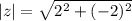
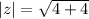
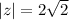
Then
`(z)/(|z|)=(1)/(√(2))+ (i)/(√(2))`

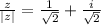
In trigonometric form,
`z=r(\cos\theta+i\sin\theta)`

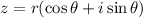
We get,
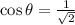`\cos\theta=(1)/(\sqrt2)` and
`\sin\theta=(1)/(\sqrt2)`

Which means
`\theta = (\pi)/(4)`

The trigonometric form is
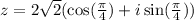`z=2√(2)(\cos((\pi)/(4))+i\sin((\pi)/(4)))`.