Question

Leigh bought a conical candle wax mold. The height of the mold is 17.7 inches and the radius of the inside of the top of the conical mold is 1.8 inches. She fills the mold completely with candle wax so that it is level with the top of the conical mold. approximately how much candle wax can the conical mold hold?

Answer 1

56.97 cubic inches

Explanation:

Answer 2

Since we wish to fill the cone, we are looking for its volume. The volume of a cone is given by the equation
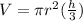
`V= \pi r^(2)( (h)/(3))` where h is the height (here 17.7 inches) and r is the radius of the top (here 1.8 inches).

We substitute the values given into the formula to obtain:

`V= \pi (1.8)^(2)( (17.7)/(3))=19.116 \pi`. This is the exact volume of the cone in cubic inches.

If you are asked instead for an approximate value you can substitute 3.14 for pi and obtain instead: 60.05469 cubic inches.