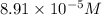Question

The concentration of so42–(aq) in a sample of river water can be determined using a precipitation titration in which a salt of ba2+(aq) is the standard solution and baso4(s) is the precipitate formed. what is the concentration of so42– (aq) in a 56.1 ml sample if 5.00 ml of a 0.00100 m ba2+(aq) solution is needed to precipitate all the so42–(aq) in the sample?

Answer 1

Answer: The concentration of sulfate ions in the solution is
`8.91* 10^(-5)M`

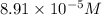
Step-by-step explanation:

To calculate the number of moles for given molarity of solution, we use the equation:

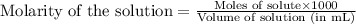`\text{Molarity of the solution}=\frac{\text{Moles of solute}* 1000}{\text{Volume of solution (in mL)}}` .......(1)

For barium ions:

Molarity of solution = 0.00100 M

Volume of solution = 5.00 mL

Putting values in equation 1, we get:

`0.00100M=\frac{\text{Moles of barium ions}* 1000}{5.00}\\\\\text{Moles of barium ions}=(0.00100* 5.00)/(1000)=5* 10^(-6)moles`

The chemical equation for the ionization of barium sulfate follows:

`BaSO_4\rightarrow Ba^(2+)+SO_4^(2-)`

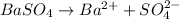
By Stoichiometry of the reaction:

1 mole of barium ions precipitate 1 mole of sulfate ions

So,
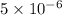`5* 10^(-6)` moles of barium ions will precipitate
`(1)/(1)* 5* 10^(-6)=5* 10^(-6)` moles of sulfate ions

Now, calculating the molarity of sulfate ions by using equation 1:

Moles of sulfate ions =
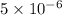`5* 10^(-6)` moles

Volume of solution = 56.1 mL

Putting values in equation 1, we get:

`\text{Molarity of sulfate ions}=(5* 10^(-6)* 1000)/(56.1)\\\\\text{Molarity of sulfate ions}=8.91* 10^(-5)M`

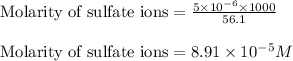
Hence, the concentration of sulfate ions in the solution is
`8.91* 10^(-5)M`

Answer 2

Hello!

The chemical reaction of the titration is the following:

Ba⁺²(aq) + SO₄⁻²(aq) → BaSO₄(s)

To calculate the concentration, we need to know the moles of SO₄⁻² in the initial solution, in the following way:


`molesSO_4^(-2)=[Ba^(+2) ]*VBa^(+2)(L)=0,001M*0,005 L \\ \\ molesSO_4^(-2)=0,000005 moles`

Now we divide the moles between the volume of the sample:


`[SO_4^(-2)]= (molesSO_4^(-2))/(V sol (L))= (0,000005 molesSO_4^(-2))/(0,0561 L)=0,000089M`

So the concentration of SO₄⁻² is 0,000089M

Have a nice day!