Question

High above the stratosphere, the atmospheric temperature may reach 1091 k. however, spacecraft and astronauts do not burn up because the concentration of molecules is very low and molecular impacts on spaceships or astronauts transfer very little energy. what is the root-mean-square velocity, in m/s, of ozone molecules at that temperature

Answer 1

The root mean square velocity of ozone molecule at temperature 1091 k is 752.9 m/s

Step-by-step explanation:

Atmospheric temperature high above the stratosphere is 1091 k. We have to find the root mean square velocity of the ozone molecule at that temperature.

Mathematically, the rms velocity is given by :

`v_(rms)=\sqrt{(3RT)/(M)}`

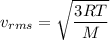
where

R is the gas constant

T is the temperature

M is the molar mass, for ozone M = 0.048 kg/mole

So,
`v_(rms)=\sqrt{(3* 8.314\ J\ K^(-1)mol^(-1)* 1091\ k)/(0.048\ kg/mol)}`

`v_(rms)=752.9\ m/s`

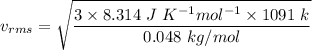
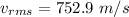
Hence, this is the required solution.

Answer 2

The root-mean-square (rms) velocity of a gas is given by:

`v_(rms) = \sqrt{ (3RT)/(M_m) }`
where T is the temperature of the gas, R is the gas constant, and M_m is the molar mass of the gas. The molar mass of ozone is

`M_m = 48.0 g/mol=0.048 kg/mol`
while the temperature of the gas in this problem is T=1091 K. By using these data and the previous equation, we can calculate the rms velocity of the molecules of ozone:

`v_(rms)= \sqrt{ (3(8.31 J K^(-1)mol^(-1))(1091 K))/(0.048 kg/mol) }=752.7 m/s`