Question

Lottery balls are thrown into a hopper and are set into motion by air forced through the container. each ball has a mass of 0.0044 kg. at one instant in time, ball 1 is moving upward with a speed of 1.3 m/s, and ball 2 is moving downward with a speed of 1.66 m/s. if the kinetic energy of the three-ball system at this instant is 0.0268 j, what must be the speed of ball 3?

Answer 1

In this three body system total kinetic energy remains constant:

`E_(k) = constant =<span>0.0268 J</span>`


`E_(k) = E_(k1)+ E_(k2)+ E_(k3)`
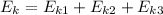
If we assume that upwards movement is positive and downwards movement is negative the formula is:

`E_(k) = E_(k1)- E_(k2)+ E_(k3)`

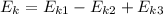
Formula for kinetic energy is:

`E_(k) = (m v^(2) )/(2)`

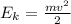
Now we have:

`E_(k) = (m v_(1) ^(2) )/(2) -(m v_(2) ^(2) )/(2) +(m v_(3) ^(2) )/(2) \\ E_(k) = (m)/(2) (v_(1) ^(2)-v_(2) ^(2)+v_(3) ^(2)) \\ \\ 0.0268= (0.0044)/(2) (1.3 ^(2)-1.66^(2)+v_(3) ^(2)) \\ \\ 0.0536=0.0022(1.69-2.7556+v_(3) ^(2)) \\ \\ v_(3) ^(2)=25.43 \\ \\ v_(3) =+-5.04`

We got two solutions: positive and negative. The speed is 5.04 m/s and direction can be upwards and downwards.