Question

Suppose the lengths of the pregnancies of a certain animal are approximately normally distributed with mean mu equals 198 daysμ=198 days and standard deviation sigma equals 20 daysσ=20 days. complete parts​ (a) through​ (f) below. ​(a) what is the probability that a randomly selected pregnancy lasts less than 191191 ​days? the probability that a randomly selected pregnancy lasts less than 191191 days is approximately

Answer 1

The probability that a randomly selected pregnancy lasts less than 191 days is approximately 0.36317.

Explanation:

Given : Suppose the lengths of the pregnancies of a certain animal are approximately normally distributed with mean mu equals 198 days and standard deviation is 20 days.

To find : What is the probability that a randomly selected pregnancy lasts less than 191 ​days?

Solution :

Mean is
`\mu=198`

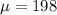
Standard Deviation
`\sigma=20`

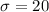
The formula to find z-score is

`z=(x-\mu)/(\sigma)`

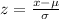
We have to find the probability that the pregnancy lasts less than 191 days.

So, x=191

Substitute the value in the formula,

`z<(191-198)/(20)`

`z<(-7)/(20)`

`z<-0.35`

Referring to z-table we find the value of z less that -0.35

Value of z less than -0.35 is 0.36317

Therefore, The probability that a randomly selected pregnancy lasts less than 191 days is approximately 0.36317.

Answer 2

We are given:
Population mean = u = 198
Population Standard Deviation = s = 20

Since population standard deviation is known, we will use z-distribution to solve this problem.

To find the probability that the pregnancy lasts less than 191 days, we have to first convert it into z score.


`z= (x-u)/(s)= (191-198)/(20)=-0.35`

So z score will be = - 0.35

From the z table, the probability of z score to be less than – 0.35 is 0.3632

Therefore, we can conclude that probability that a randomly selected pregnancy lasts less than 191 days is approximately 0.3632.