Answer:
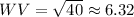
Explanation:
We have been given a graph of coordinate plane. We are asked to find the length of segment WV.
Point W(-2,-2) and point V(0,4).
We will use distance formula to solve our given problem.

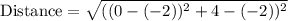
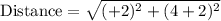
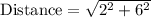
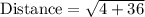
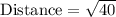

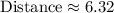
Therefore, the length of segment WV is approximately 6.32 units.