Answer: 0.4920238
Explanation:
Given: z is a standard normal variable.
We know that probability of z lies lies between two values a and b is given by :-
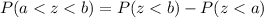
Now, the probability that z lies between -2.41 and 0 is given by :-
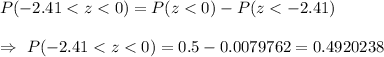 [By using z-table for standard normal distribution]
[By using z-table for standard normal distribution]
Hence, the probability that z lies between -2.41 and 0 = 0.4920238