Answer:
Option 4 - (15+x)(12+x)=(15)(12)+160
Explanation:
Given : The Davidson family wants to expand its rectangular patio, which currently measures 15 ft by 12 ft. They want to extend the length and width the same amount to increase the total area of the patio by 160 ft sq.
To find : Which quadratic equation best models the situation?
Solution :
Dimension of rectangular patio is
Length = 15 ft.
Width = 12 ft.
Let x be the expansion of length and width of the rectangular patio.
So, The new length of the rectangular patio is (x+15).
The new width of the rectangular patio is (x+12).
We know, Area of rectangle = Length × Width
According to question,
They want to extend the length and width the same amount to increase the total area of the patio by 160 ft sq.
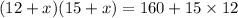
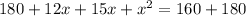
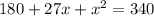

Therefore, The required quadratic equation is
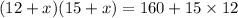
Hence, Option 4 is correct.