Answer:
tanx =
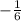
Explanation:
hey there,
< You have to memorize trigonometric identities for this. Here's the one we'll use for this problem.
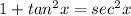
Plug in the sec since we already know what it is.
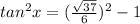
When you square it, you get 37/36. 37/36-1 = 1/36
tan^2x = 1/36
Since it's squared, let's find the square root of 1/36.
It would be +- 1/6.
Since sinx < 0, it has to be -1/6. >
Hope this helped! Feel free to ask anything else.