Question

SOMEONE HELP!!!! I FAILED THIS ON PLATO 10 TIMES I NEED THE CORRECT ANSWER

Round your answers to the nearest thousandth. The probability that Sandra gets a ride to work on any morning is 0.7. The probability that she gets a ride 3 times in a 5-day work week is____, and the probability that she gets a ride at least 2 times in a 5-day workweek is____.

Answer 1

The probability that she gets a ride 3 days in the week is 0.309. The probability that she gets a ride to work at least 2 times in the week is 0.969.

This is binomial, as there are two outcomes, the probability of one happening does not affect the other, and there is a fixed number of trials.

For three rides to work that week,

`_nC_r(p)^r*(1-p)^(n-r) \\ \\_5C_3(0.7)^3(1-0.7)^(5-3)=(5!)/(3!2!)(0.7)^3(0.3)^2=0.3087\approx0.309`

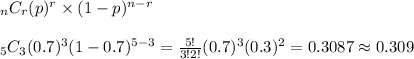
To find the probability that she gets a ride at least twice that week, we first find the probability that she does not get a ride at all that week or she only gets a ride one day; then we subtract that from 1:


`1-[P(X=0)\text{ or }P(X=1)] \\ \\=1-(_5C_0(0.7)^0(1-0.7)^(5-0)+_5C_1(0.7)^1(1-0.7)^(5-1)) \\ \\=1-((5!)/(0!5!)(0.7)^0(0.3)^5+(5!)/(1!4!)(0.7)^1(0.3)^4) \\ \\=1-(0.00243+0.02835)=1-0.03078=0.96922\approx0.969`