Question

Suppose that x is normally distributed with mean 110 and standard deviation 30.

a. what is the probability that x is greater than 170?

Answer 1

Standard the random variable
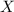
`X` using the transformation


`Z=\frac{X-\mu}\sigma`

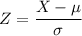
where
`\mu` and
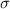
`\sigma` are the mean and standard deviation of
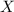
`X`, respectively.


`\mathbb P(X\ge170)=\mathbb P\left((X-110)/(30)\ge(170-110)/(30)\right)=\mathbb P(Z\ge2)`

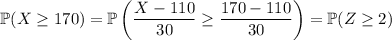
Now, you can recall that for any normal distribution, approximately 95% of its data falls within 2 standard deviations of the mean, so to either side, there is approximately 2.5% of data that falls below 2 standard deviations from the mean, and 2.5% that falls
`2\sigma` above
`\mu`. In other words,
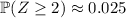
`\mathbb P(Z\ge2)\approx0.025`.