Question

Use the method of lagrange multipliers to find

a. the minimum value of x + y​, subject to the constraints xy=64, x>0, y>0

Answer 1

The Lagrangian,


`L(x,y,\lambda)=x+y+\lambda(xy-64)`

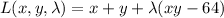
has partial derivatives (set equal to 0)


`L_x=1+\lambda y=0\implies\lambda=-\frac1y`

`L_y=1+\lambda x=0\implies\lambda=-\frac1x`

`L_\lambda=xy-64=0`

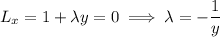
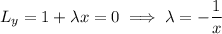
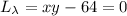
The first two equations tell us that
`-\frac1y=-\frac1x\implies x=y`.

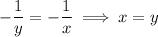
Substituting this into the second equation, we have


`xy-64=0\iff x^2=0\implies x=\pm8\implies\begin{cases}x=8,y=8\\x=-8,y=-8\end{cases}`

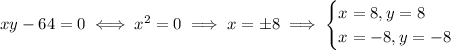
We have that
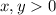
`x,y>0`, so we only have the one critical point on the surface
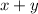
`x+y` at (8, 8), with an extreme value of 16.