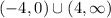Question

Consider the equation below. (if an answer does not exist, enter dne.) f(x) = x4 − 32x2 + 5 (a) find the interval on which f is increasing. (enter your answer using interval notation.)

Answer 1

The intervals of increase are
`\left(-4, 0\right) \cup \left(4, \infty\right)`

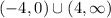
Explanation:

When a function is increasing, its derivative is positive. So if we want to find the intervals where a function increases, we differentiate it and find the intervals where its derivative is positive.

Let's find the intervals where
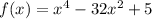`f(x) = x^4 -32x^2 + 5` is increasing.

First, we differentiate f(x)

`(d)/(dx) f = (d)/(dx) (x^4 -32x^2 + 5)\\(d)/(dx) f = (d)/(dx)\left(x^4\right)-(d)/(dx)\left(32x^2\right)+(d)/(dx)\left(5\right)\\(d)/(dx) f =4x^3-64x`

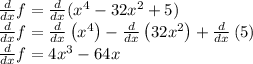
Now we want to find the intervals where
`(d)/(dx) f` is positive This is done using critical points, which are the points where
`(d)/(dx) f` is either 0 or undefined.

`4x^3-64x=0\\4x\left(x^2-16\right)=0\\4x\left(x+4\right)\left(x-4\right)=0\\\\\mathrm{The\:solutions\:are}\\x=0,\:x=-4,\:x=4`

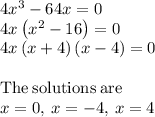
These points divide the number line into four intervals

`(-\infty,-4);(-4,0);(0,4);(4,\infty)`

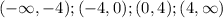
Let's evaluate
`(d)/(dx) f` at each interval to see if it's positive on that interval.

`\left\begin{array}{cccc}Interval&x-value&(d)/(dx)f& Verdict\\x<-4&-5&-180&Decreasing\\-4<x<0&-1&60&Increasing\\0<x<4&1&-60&Decreasing\\x>4&5&180&Increasing\end{array}\right`

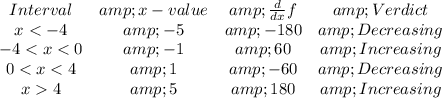
The intervals of increase are
`\left(-4, 0\right) \cup \left(4, \infty\right)`

Answer 2

The function f(x) is increasing on the interval (-4, 0) ∪ (4, ∞).