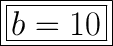Answer:
b = 10
Explanation:
When two quantities vary inversely, one quantity increases as the other decreases, and their product remains constant.
Therefore, if b varies inversely with h, then:

where k is the constant of proportionality.
Given b = 8 when h = 5, then:
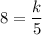
Solve for k:
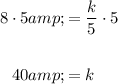
Therefore, the equation that links h to b is:

To find the value of b when h = 4, substitute h = 4 into the equation:
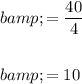
Therefore, the value of b when h = 4 is: