Part a)Total Number of doctors in sample = n = 356
Number of doctors with solo practice = x = 175
Proportion of doctors with solo practice = p =
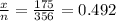
q = 1 - p = 0.508
As both p and q are approximately 0.5, as a new writer the percentage of survey results will be reported as:
About half of the medical doctors opt for the solo practice.
Part b)Margin of Error for 90% confidence interval.z score = 1.645
Margin of Error = E
Formula for Margin of Error is:
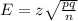
Using the values in the formula,we get:
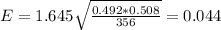
Therefore, the margin of error based on 90% confidence interval is 0.044.