Question

Two consecutive whole number that square root a of 59 lies between?

Answer 1

Between 7 and 8. (7x7=49) and (8x8=64). Since 59 is between 49 and 64, the square root of 59 lies between 7 and 8.

Answer 2

`7<√(59)<8`

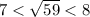
Explanation:

We are asked to find two consecutive integers such that square root a of 59 lies between them.

We know that perfect square less than square root of 59 is square root of 49, which is square of 7.

The perfect square greater than square root of 59 is square root of 64, which is square of 8.

`√(49)<√(59)<√(64)`

`√(7^2)<√(59)<√(8^2)`

`7<√(59)<8`

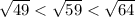
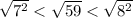
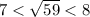
Therefore, square root of 59 lies between 7 and 8.