Question

Write an equation of the line that is perpendicular to 3x + 9y = 7 and passes through the point (6, 4).

Answer 1

Hi there!

The equation of any line perpendicular to

`ax + by = c`
is

`bx - ay = c`

Therefore, in this situation, the formula of the line would be

`9x - 3y = c`

Given that the line passes through the point (6, 4) we get

`9 * 6 - 3 * 4 = c`

`54 - 12 = c`

`c = 44`

Therefore, the equation of the line that is perpendicular to 3x + 9y = 7 and passes through (6, 4) is

`9x - 3y = 44`

Answer 2

Answer: The equation of the line is
`3x-y=14.`

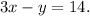
Step-by-step explanation: We are given to find the equation of the line that is perpendicular to 3x + 9y = 7 and passes through the point (6, 4).

The slope-intercept form of the given equation is

`3x+9y=7\\\\\Rightarrow 9y=-3x+7\\\\\Rightarrow y=-(1)/(3)x+(7)/(9).`

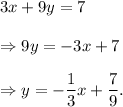
So, slope will be given by

`m=-(1)/(3).`

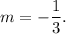
If 'p' represents the slope of the perpendicular line, then we must have

`m* p=-1\\\\\Rightarrow -(1)/(3)* p=-1\\\\\Rightarrow p=3.`

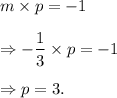
Therefore, the equation of the line with slope p = 3 and passing thjrogh the point (6, 4) is given by

`y-4=p(x-6)\\\\\Rightarrow y-4=3(x-6)\\\\\Rightarrow y-4=3x-18\\\\\Rightarrow 3x-y=14.`

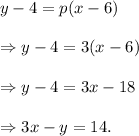
Thus, the required equation of the line is [tex]3x-y=14.[/tex]