Answer: The correct option is (B) (4, 9).
Step-by-step explanation: We are given to use the elimination method to solve the following system of equations :

Multiplying equation (i) by 2, we have
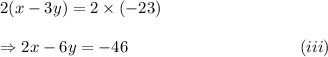
Adding equations (ii) and (iii), we get
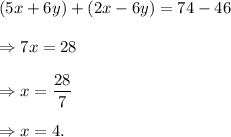
From equation (i), we again get
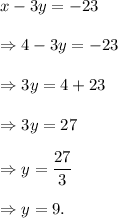
Thus, the required solution of the given system is (x, y) = (4, 9).
Option (B) is CORRECT.