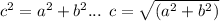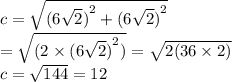Question

Find the hypotenuse of each isosceles right triangle when the legs are of the given measure. 6 sqrt 2

Answer 1

Isosceles right triangles have two equal sides (a and b) that are not the hypotenuse (c). And when two sides are equal, so are their opposite angles. There are only 180° degrees in any triangles, thus the right angle = 90°, so 90 left for the two equal, means that 2x=90,
x = 45°.

There are several ways to go about solving a triangle like this. The best and easiest is simply to memorize that the hypotenuse is exactly root2 times the other sides. Or, each isosceles side is the hypotenuse (c) ÷ root2

`a = b = c / √(2) \\ c = a√(2) \\ c = 6 √(2) * √(2) = 6 * 2 = 12`
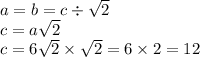
Another way to do it is the longer proof of Pythagorean Theorem:

`{c}^(2) = {a}^(2) + {b}^(2)... \: \: c = \sqrt{({a}^(2) + {b}^(2))} \\`

`c= \sqrt{({6 √(2)) }^(2) + ({6 √(2))}^(2)} \\ = \sqrt{(2 *{(6 √(2) )}^(2) )} = √(2(36 * 2)) \\ c = √(144) = 12`