Question

A triangle has an area of 88 square inches. Find the length of the base if the base is 5 inches more than the height.

Answer 1

The base is 16 inches.

The formula for the area of a triangle is

A = 1/2bh

We know that b = h+5, so we can rewrite this as:

A = 1/2(h+5)(h)

Using the area that we have, we now have:

88 = 1/2(h+5)(h)

We can cancel the 1/2 by multiplying by 2:
88*2 = (1/2)(h+5)(h)*2
176 = (h+5)(h)

Using the distributive property, we have:
176 = h² + 5h

We want quadratic equations to be set equal to 0, so we will subtract 176 from both sides:
176 - 176 = h² + 5h - 176
0 = h² + 5h - 176

Using the quadratic formula:

`h=(-b\pm √(b^2-4ac))/(2a) \\ =(-5\pm √(5^2-4(1)(-176)))/(2(1))=(-5\pm √(25--704))/(2) \\ \\=(-5\pm √(25+704))/(2)=(-5\pm √(729))/(2) \\ \\=(-5\pm 27)/(2)=(-5-27)/(2)\text{ or }(-5+27)/(2) \\ \\=(-32)/(2)\text{ or }(22)/(2)=-16\text{ or }11`

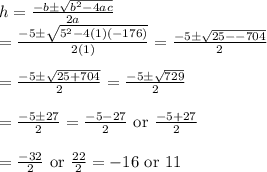
Since a negative length makes no sense, we know that h=11.

The base is 5 inches longer than the height, so b = 11+5 = 16.