Question

James paints the outside of his house. He leans a 13 -foot ladder against the house. The base of the ladder is 5 feet away from the house. Which expression can be used to determine the distance from the base of the house to the top of the ladder?

Answer 1

The distance from the base of the house to the top of the ladder is 12 feet. The expression used to determine the distance from the base of the house to the top of the ladder is
`y = \sqrt{l^(2)-x^(2)}`.

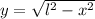Explanation:

Let suppose that the ground is perpendicular to the wall of the house, then we can represent the system formed by the ladder, the wall of the house and the ground in the form of a right triangle, whose hypotenuse (length of the ladder) is determine by Pythagorean Theorem:

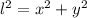`l^(2) = x^(2)+y^(2)` (1)

Where:

`x` - Distance from the base of the house to the base of the ladder, measured in feet.

`y` - Distance from the base of the house to the top of the ladder, measured in feet.

`l` - Length of the ladder, measured in feet.

If we know that
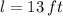`l = 13\,ft` and
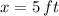`x = 5\,ft`, then the distance from the base of the house to the top of the ladder is:

`y = \sqrt{l^(2)-x^(2)}`

`y = \sqrt{(13\,ft)^(2)-(5\,ft)^(2)}`

`y = 12\,ft`

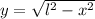
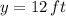
The distance from the base of the house to the top of the ladder is 12 feet. The expression used to determine the distance from the base of the house to the top of the ladder is
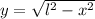`y = \sqrt{l^(2)-x^(2)}`.