Question

What is the 6th term of the geometric sequence where a1 = -4096 and a4 = 64?

Answer 1

`\bf \begin{array}{llccll} term&value\\ \text{\textemdash\textemdash\textemdash}&\text{\textemdash\textemdash\textemdash}\\ a_1&-4096\\ a_2&-4096r\\ a_3&-4096rr\\ a_4&-4096rrr\\ &-4096r^3\\ &64 \end{array}\implies -4096r^3=64 \\\\\\ r^3=\cfrac{64}{-4096}\implies r^3=-\cfrac{1}{64}\implies r=\sqrt[3]{-\cfrac{1}{64}} \\\\\\ r=\cfrac{\sqrt[3]{-1}}{\sqrt[3]{64}}\implies \boxed{r=\cfrac{-1}{4}}\\\\ -------------------------------`


`\bf n^(th)\textit{ term of a geometric sequence}\\\\ a_n=a_1\cdot r^(n-1)\qquad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ r=\textit{common ratio}\\ ----------\\ r=-(1)/(4)\\ a_1=-4096\\ n=6 \end{cases} \\\\\\ a_6=-4096\left( -(1)/(4) \right)^(6-1)\implies a_6=-4^6\left( -(1)/(4) \right)^5`

Answer 2

The sixth term of the geometric sequence is 4.

Explanation:

Given : Geometric sequence term are
`a_1=-4096` and
`a_4=64`

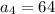
To find : What is the 6th term of geometric sequence ?

Solution :

`a_1=-4096`

We know, fourth term is
`a_4=ar^3`

`a_4=64`

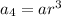
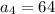
So,
`64=(-4096)r^3`

`(64)/((-4096))=r^3`

`-0.015625=r^3`

`r=(-0.015625)^{(1)/(3)}`

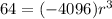
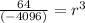
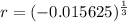
The sixth term is
`a_6=ar^5`

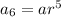
Substitute,

`a_6=(-4096)((-0.015625)^{(1)/(3)})^5`

`a_6=-4096((-0.015625)^{(5)/(3)})`

`a_6=-4096(-0.0009765625)`

`a_6=4`

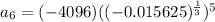
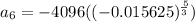
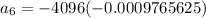
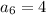
Therefore, The sixth term of the geometric sequence is 4.