Question

The area of a rectangle is 44ft^2, and the length of the rectangle is 3ft less than twice the width. Find the dimensions of the rectangle

Answer 1

The formula for the area of a rectangle is A = L(length) × W(width)
A = L × W
Plug in the information:
A = 44, L = 2W - 3 b/c less than means switch the order before subtracting, W = W
44 = (2W - 3)×W
44 = 2W² - 3W ← used the distributive property... This is a quadratic equation
2W² - 3W - 44 = 0 ← collect all terms on one side so we can use some method to solve a quadratic equation... like factoring or quadratic formula
Note any negative values will be discarded because dimensions are measurements and they are not negative

Factoring: (2W - 11)(W + 4) = 0
2W - 11 = 0 solves to W = 5.5
W + 4 = 0 solves to W = -4 ←must discard
So W = 5.5 and L = 2(5.5) - 3 = 8
You can check the values to see if they equal 44 when plugged into Area formula
ANSWER: Dimensions 8 ft by 5.5 ft

Answer 2

Hi there! The width of the rectangle is 5.5ft and the length is 8ft.

Let the width of the rectangle be represented by X. This learns us the length of the rectangle is 2X - 3.

Therefore the area of the rectangle (which is length * width) would be

`x(2x - 3) = {2x}^(2) - 3x`
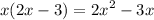
Since the area of the rectangle is 44 ft^2, we end up with the following equation.


`2 {x}^(2) - 3x = 44`

`2 {x}^(2) - 3x - 44 = 0`


`x = \frac{3 + \sqrt{( - 3) {}^(2) - 4 * 2 * - 44} }{4}`

`x = (3 + √(361) )/(4)`

`x = (3 + 19)/(4) = (22)/(4) = 5 (1)/(2)`

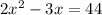
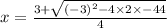
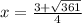
OR


`x = \frac{3 - \sqrt{( - 3) {}^(2) - 4 * 2 * - 44} }{4}`

`x = (3 - √(361) )/(4)`

`x = (3 - 19)/(4) = ( - 16)/(4) = - 4`

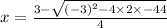
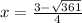
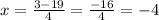
Since X represents the width (and width can't be negative), the width of the rectangle is 5.5ft

The length is
2X - 3 = 2 × 5.5 - 3 = 11 - 3 = 8ft.