Question

Solve the equations
x squared + y squared = 36
x = 2y + 6

Answer 1

Given the equations:

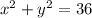`x^2+y^2 =36` .....[1]

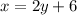`x =2y +6` ....[2]

Substitute the value of x in [1] we get;'

`(2y+6)^2+y^2 =36`

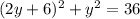
Use identity:
`(a+b)^2= a^2+2ab+b^2`

`4y^2+36+24y + y^2 =36`

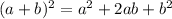
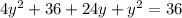
Combine like terms;

`5y^2+36+24y=36`

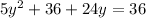
Subtract 36 from both sides we get;

`5y^2+24y=0`

`y (5y+24) = 0`

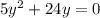
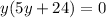
By zero product property, we get;

y = 0 and
`y =- (24)/(5) = -4.8`

Substitute these y values in [2] to get x values;

For y = 0 we have;

x = 2(0) +6 = 0+6 = 6

For x = -4.8

x = 2(-4.8)+6 = -9.6 + 6 = -3.6

Therefore, the solution for the given equations are; (6, 0) and (-3.6, -4.8)