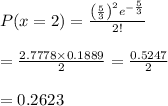Question

The distance between consecutive flaws on a roll of sheet aluminum is exponentially distributed with a mean distance of three meters.

a.what is the mean number of flaws per meter?b.what is the probability that we inspect the next six meters before finding a flaw?c.what is the probability that a five meter length of aluminum contains exactly two flaws?

Answer 1

Part a:

Given that the mean distance between consecutive flaws on a roll of sheet aluminum is 3 meters, thus the rate parameter (the mean number of flaws per meter) is given by 1 divided by the mean distance = 1 / 3 = 0.333

Part b:


`P(x>k)=e^(-\lambda k)`

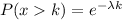
Thus,


`P(x>6)=e^{- (1)/(3) (6)} \\ \\ = e^(-2)= 0.1353`

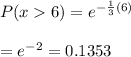
Therefore, the probability that we inspect the next six meters before finding a flaw is 0.1353.


Part c:

In a 5 metre length of aluminium, the mean distance between consecutive flaws is given by 5 x 1/3 = 5/3.

The probability that the five meter length of aluminum contains exactly two flaws is given by the poisson distribution with a mean of 5/3.


`P(x=2)=\frac{\left( (5)/(3) \right)^2e^{-(5)/(3) }}{2!} \\ \\ = (2.7778*0.1889)/(2) = (0.5247)/(2) \\ \\ =0.2623`