Question

Two constructors working together finished building a room in 6 days. how long would it take for each constructor to build the room by himself, if it is known that one of them would require 9 more days than the other?

Answer 1

It would take one construction worker 9 days and the other 18 days.

Let x be the number of days the first construction worker takes to build the room by himself. If x were 2, he could build 1/2 of the room in the time limit, etc...so 1/x will be the portion of the room he can build by himself in the given tie limit.

The second construction worker can build 1/(x+9) of the room by himself in the given time limit.

Together, we have the equation
1/x(6) + 1/(x+9)(6) = 1

[The speed of the first contractor times the number of days, and the speed of the second contractor times the number of days; together they build 100% of the room]

This gives us

6/x+ 6/(x+9) = 1

We will multiply everything by x to get it off of the denominator:
6/x(x) +(6/(x+9))(x)= x
6 + 6x/(x+9) = x

Multiply everything by x+9 now:

6(x+9) + (6x/(x+9))(x+9) = x(x+9)
6x + 54 + 6x = x² + 9x
12x + 54 = x² + 9x

Subtract 12x from each side:
12x + 54 - 12x = x²+9x-12x
54 = x²-3x

Subtract 54 from each side:
54-54 = x²-3x-54
0 = x²-3x-54

This factors easily; -9(6) = -54 and -9+6 = -3:
0 = (x-9)(x+6)

Using the zero product property we know either x-9=0 or x+6=0; this gives us x=9 or x=-6. Negative time makes no senses, so x=9 hours.

This means the slower contractor takes 9+9 = 18 hours.

Answer 2

It would take 10 days to the first constructor and 15 days to the second one to finish the room.

Explanation:

Time to finish the room with both constructors: 6 days.

Time to finish the room by the first constructor only: x days.

Time to finish the room by the second constructor only: (x + 5) days.

If we associate all that, 1 day work of both constructors working at the same time would be
`(1)/(6)`

1 day work of the first is:
`(1)/(x)`

1 day work of the second is:
`(1)/(x+5)`

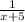
Now, we need to find the variable, using the following equation

`(1)/(x)+(1)/(x+5)=(1)/(6)\\(x+5+x)/(x^(2) +5x) =(1)/(6)\\12x+30=x^(2) +5x\\ x^(2) +5x-12x-30=0\\ x^(2) -7x-30=0`

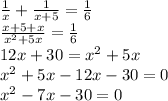
Then, we need to find two numbers which product is 30, and which difference is 7. Those numbers are 10 and 3, because 10 times 3 is 30, and 10 minus 3 is 7.

`x^(2) -7x-30=(x-10)(x+3)=0`

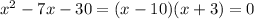
Using the zero factor property, we have

`x-10=0 \implies x=10\\x+3=0 \implies x=-3`

But, only the positive number makes sense. Replacing the value in each expression we have

First constructor:
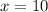`x=10` days.

Second constructor:
`x+5=10+5=15` days,

Threfore, it would take 10 days to the first constructor and 15 days to the second one to finish the room.