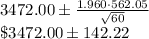Every confidence interval has associated z value. As confidence interval increases so do the z value associated with it.
The confidence interval can be calculated using following formula:
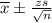
Where
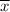
is the mean value, z is the associated z value, s is the standard deviation and n is the number of samples.
We know that standard deviation is simply a square root of variance:
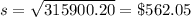
The confidence interval of 95% has associated z value of
1.960.
Now we can calculate the confidence interval for our income: