Question

Fifty-six percent of all american workers have a workplace retirement plan. if americans retirement plans are independent, what is the probability that exactly 3 out of 5 randomly selected americans will have a retirement plan

Answer 1

The probability would be 0.34 or 34%.

We will set this up as a binomial distribution:

Answer 2

We have been given that 56 percent of all American workers have a workplace retirement plan and we are also given that Americans retirement plans at workplace are independent.

To find out probability of exactly 3 out of 5 randomly selected Americans will have a retirement plan we will use Bernoulli trials.

`_(r)^(n)\textrm{c}\cdot p^(r)\cdot q^(n-r)`

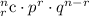
where p is probability of a success which in this case is Americans that have workplace retirement plans and q is probability of failure which in this case are Americans that don't have workplace retirement plans.

Upon substituting our given values in this formula we will get,

`_(3)^(5)\textrm{c}\cdot0.56^(3)\cdot 0.44^((5-3))`

`_(3)^(5)\textrm{c}\cdot0.56^(3)\cdot 0.44^(2)`

`(5!)/(2!3!)\cdot0.175616\cdot 0.1936`

`(5\cdot 4\cdot 3!)/(2\cdot 1\cdot 3!)\cdot 0.56^(3)\cdot 0.44^(2)`

`10\cdot 0.175616\cdot 0.1936=0.339992576`

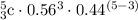
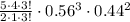
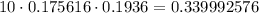
Rounding our answer to nearest hundredth we get our probability that exactly 3 out of 5 randomly selected Americans will have a retirement plan is 0.34.