Question

What is the solution of the equation sqrt 2x+13-5=x?

Answer 1

2x-x=-13+5
x=-8
I think so
Good luck

Answer 2

Answer: The solution is x = -2.

Step-by-step explanation: The given equation is as follows:

`√(2x+13)-5=x.`

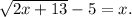
We will be using the following algebraic identities:

`(i)~(a+b)^2=a^2+2ab+b^2,\\\\(ii)~(√(a+b))^2=a+b.`

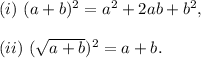
The solution is as follows:

`√(2x+13)-5=x\\\\\Rightarrow √(2x+13)=x+5\\\\\Rightarrow (√(2x+13))^2=(x+5)^2\\\\\Rightarrow 2x+13=x^2+10x+25\\\\\Rightarrow x^2+8x+12=0\\\\\Rightarrow x^2+6x+2x+12=0\\\\\Rightarrow x(x+6)+2(x+6)=0\\\\\Rightarrow (x+2)(x+6)=0\\\\\Rightarrow x+2=0,~~~~~~x+6=0\\\\\Rightarrow x=-2,~-6.`

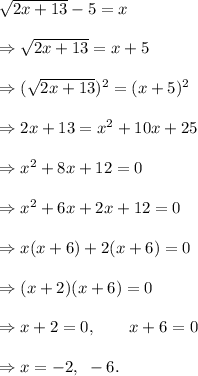
If we substitute x = -2, then

`L.H.S=√(2* (-2)+13)-5=\sqrt9-5=3-5=-2=R.H.S.`

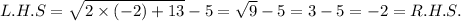
Ie we substitute x = -6, then

`L.H.S=√(2* (-6)+13)-5=\sqrt1-5=1-5=-4\\eq -6=x=R.H.S.`

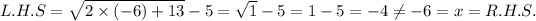
Since x = -6 does not satisfy the given equation, so the solution is x = -2.

Thus, the solution is x = -2.