Question

Given that kx^2 + hx - 4 = 0 has no roots. Find the ranges of value of k

Answer 1

The ranges of value of k are values larger than 0 and lower than 16.

Explanation:

Suppose we have a second order polynomial in the following format:

`ax^2 + bx + c = 0, a \\eq 0`

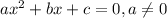
It will have no roots if:

`\Delta = b^2 - 4ac < 0`

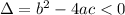
In this question, we have that:

`hx^2 + hx - 4 = 0`

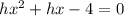
So, the coefficients are:

`a = h, b = h, c = -4`

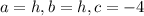
Then

`\Delta < 0`

`b^2 - 4ac < 0`

`h^2 - 16h < 0`

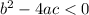
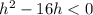
A quadratic function, with a positive(as is 1 in this inequality), will be negative between it's roots.

The roots are:

`h^2 - 16h = 0`

`h(h - 16) = 0`

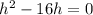
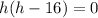
So

h = 0 or h = 16.

The ranes of value of k are values larger than 0 and lower than 16.