Answer:
The ranges of value of k are values larger than 0 and lower than 16.
Explanation:
Suppose we have a second order polynomial in the following format:
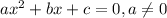
It will have no roots if:
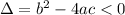
In this question, we have that:
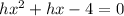
So, the coefficients are:
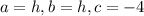
Then
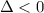
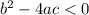
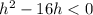
A quadratic function, with a positive(as is 1 in this inequality), will be negative between it's roots.
The roots are:
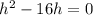
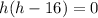
So
h = 0 or h = 16.
The ranes of value of k are values larger than 0 and lower than 16.