Answer:Sum = 49/6
Step-by-step explanation:The geometric sequence has the following form:
a1 + a1*r + a1*r² + a1*r³ + ..... etc
The sum of the infinite geometric sequence can be computed as follows:
S =
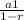 1- getting r:
1- getting r:The given sequence is:
7 + 1 + 1/7 + 1/49 + .....
This means that:
a1 = 7
a1 * r = 1
7r = 1
r = 1/7
We can double check this value using another term:
a1 = 7
a1 * r² = 1/7
7 * r² = 1/7
r² = (1/7) / (7)
r² = 1/49
r = 1/7
2- getting the sum:Now we have:
a1 = 7
r = 1/7
Substitute with these givens in the above equation to get the sum as follows:
S =
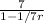
S = 49/6
Hope this helps :)