Answer:
B.
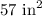
Explanation:
We have been that apothem of a regular octagon is 4.2 inches and length of each side is 3.4 inches. We are asked to find the area of our given octagon.
We know that area of octagon is half the product of perimeter and apothem of the octagon.
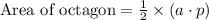 , where,
, where,
a = Apothem of octagon,
p = perimeter of octagon.
We will find perimeter of our given octagon by multiplying length of each side by 8.
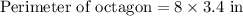
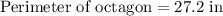

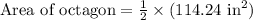
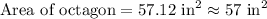
Therefore, the area of our given octagon is 57 square inches and option B is the correct choice.